Benford's Law Is The Most Interesting Thing You've Never Heard About
I have been in a phase lately where I just like learning things. I was saying on Friday Night Pints yesterday how I wish it was easier to learn new things as an adult. In college, it feels like you're basically forced to learn things. You're not actually absorbing anything because it feels like you're just trying to memorize a bunch of stuff so you can regurgitate it on tests and papers so you can get a good GPA, not lose your scholarship, get a good job, make money, etc. But when you're an adult out of school, cue my cheesy teacher voice, learning can be FUN!
I've been falling down a ton of YouTube rabbit holes lately about a wide variety of topics. One thing that particularly caught my interest last week was something called "Benford's Law." I watched a Netflix thing about it from the show "Connected" and that kind of stunk to be honest. But it introduced the topic to me and I then watched more YouTube videos and read more stuff about it. I will do my best to explain it because I personally find it fascinating.
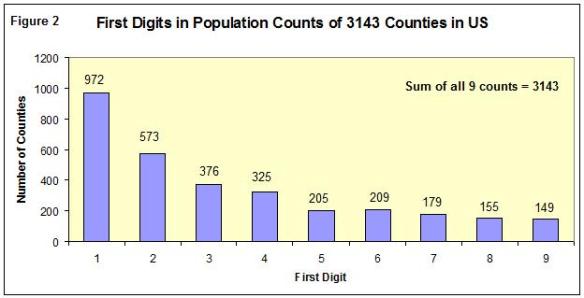
It basically says that "random" numbers aren't as random as you would think when it comes to the first digit. If you're sampling data about something (populations, sports stats, social media followings, raffle tickets, stocks, your finances, etc.), you might think that the first digit has basically a 1 in 9 chance (~11%) to be any number from 1 through 9. Well, Benford's Law says that's not actually true. Instead, first digits all follow a pattern. It's more likely the first digit will be 1 than 2. And 2 than 3. And 3 than 4. And so on and so forth. There's basically 1 in 3 chance that the first digit will be a 1. And just a 1 in 20 chance the first digit will be a 9. Here is the chart that goes along with it.
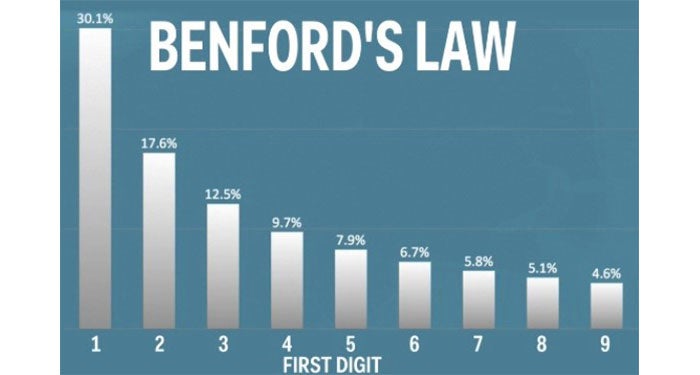

Advertisement
At first, it seems ridiculous. But it's proven to be true in millions of real world examples. It's so accurate, in fact, that the IRS apparently uses it to detect if people are committing tax fraud. It's been used as evidence in criminal cases. It can be used to detect election fraud. Numbers and math are cool to me, and the fact that there's this seemingly random trend that exists throughout all the numbers in the universe and has real world applications is fascinating.
If my explanation isn't clear enough, watch this video from someone way smarter than me. He also has a really cool accent.
There's a bunch of other videos about it you can watch if you fall down the rabbit hole, but that's the video with the easiest explanation from what I've seen. And it does kind of make sense. You have to get to 1 before you get to 2 and 2 before you get to 3 and 3 before you get to 4, etc. So if you're just going to stop/cut-off counting somewhere, it's more likely you'll stop at something with the first digit 1 before it can get to the first digit 2.
And his other explanation just sort of intuitively makes sense too. Let's use a city's population for example. For a city with a population of 100,000 to grow into a new first digit (200,000), it would have to double in size (100% increase). For a city with a population of 900,000 to grow into a new first digit (1,000,000), it only has to increase in size by 11.1% to get us back to 1 as that leading digit. So the chart just makes sense to my brain when I think of it that way.
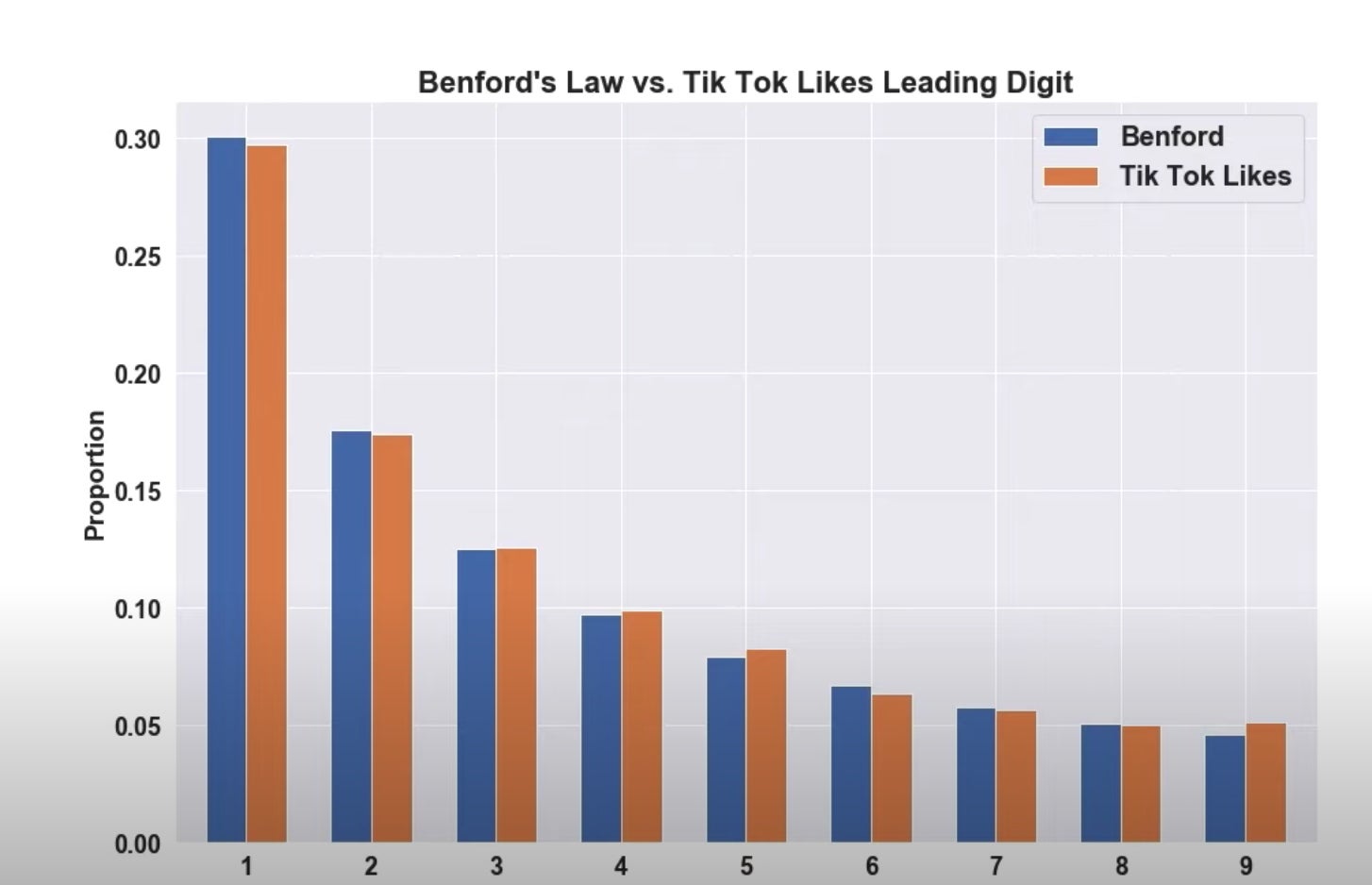
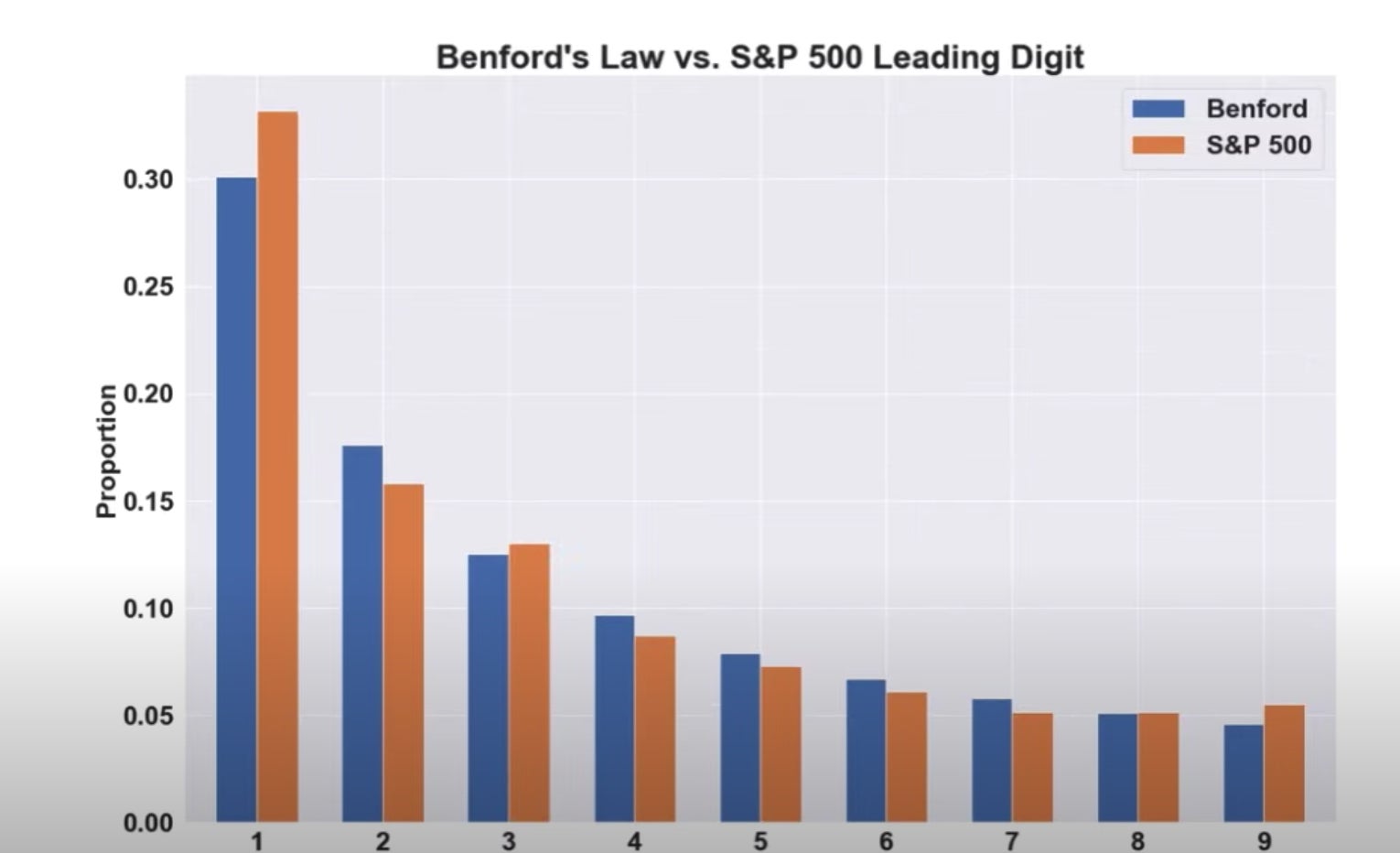
Here's a video of it being applied to things like TikTok likes and stock prices.
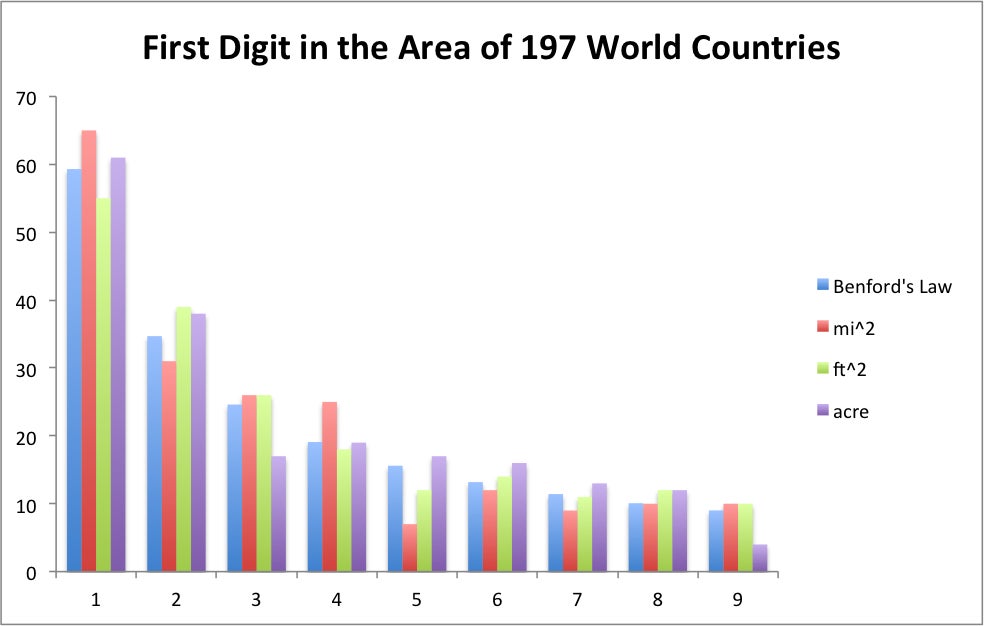
Now as you see in that video, it obviously can't work on everything. Ages of NBA players are pretty much exclusively going to be 20s and 30s. Another example would be if you do heights of people, you're pretty much exclusively looking between 60 and 70 inches. But for large data sets where numbers aren't congested in small concentrations, Benford's Law will apply. These charts are pretty crazy.

Advertisement

Advertisement
Maybe this all bores you and you don't care. Or maybe you'll be like me and find this interesting. At the very least, I hope this is a lesson on how to cheat on your taxes so you don't get caught by the IRS.
